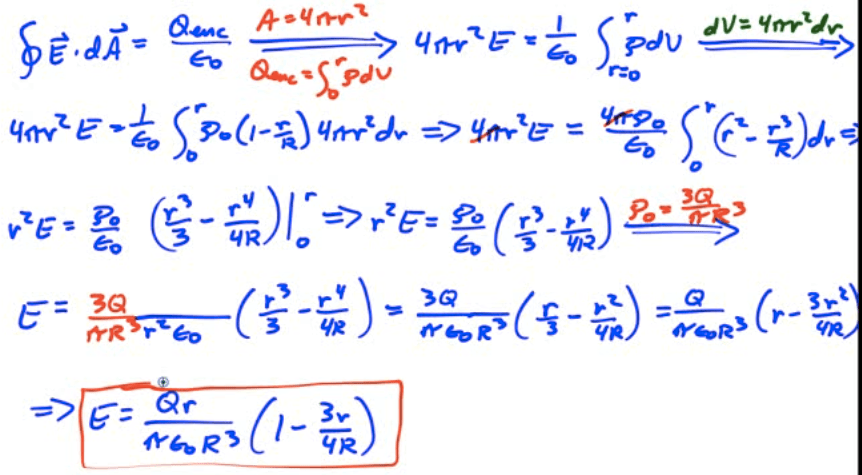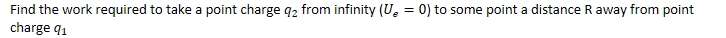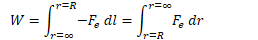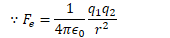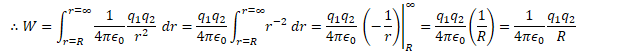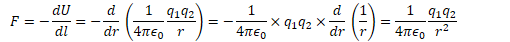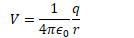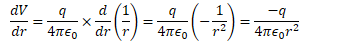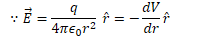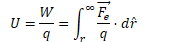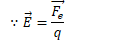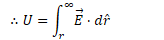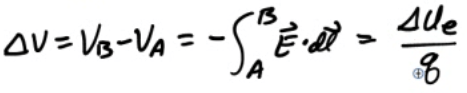Electric Potential Energy

  • When an object was lifted against gravity by applying a force for some distance, work was done to give that object gravitational potential energy

  • When a charged object is moved against an electric field by applying a force for some distance, work is done to give that object electric potential energy.

  • The work done per unit charge in moving a charge between two points in an electric field is a scalar known as the electric potential V (or voltage)

    • Units: volts (1V = 1 J/C)

    • The work done is equal to the change in the object's electric potential energy (UE)

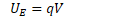
    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image078.png

    Electric Potential Energy Work Kinetic Energy W = Fd = q(Ed) = qV= mgh = 7 mv2 Force Voltage Gravitational Electric Field Potential Energy velocity

The Electron-Volt

  • Oftentimes the electrical energy and/or work done is a very small portion of a joule

  • A smaller, alternative, non-standard unit of energy is often used for convenience, known as the electron volt (eV)

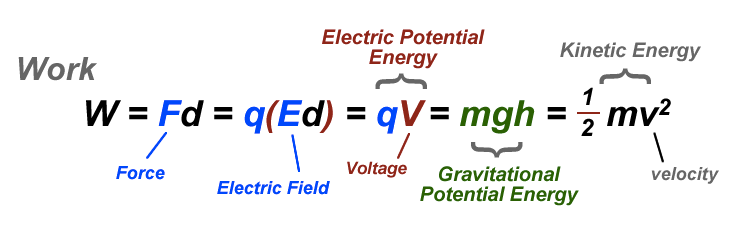
    • 1 eV is the amount of work done in moving an elementary charge through a potential difference of 1 volt

    • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image080.png

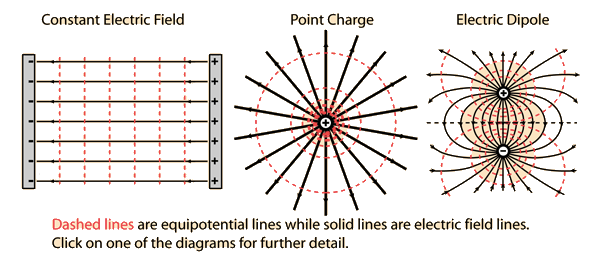
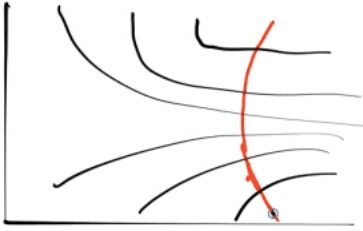
Equipotential Lines

  • Topographic maps show you lines of equal altitude, or equal gravitational potential

  • Lines connecting points of equal electrical potential are known as equipotential lines.

    • Equipotential lines always cross electrical field lines at right angles

    • If you move a charged particle in space, and stay on an equipotential line, no work will be done.

    • As equipotential lines get closer together, the gradients of the potential increases (stepper "slope" of potentials)

    • Electric field points from high to low potential

    Constant Electric Field Point Charge Electric Dipole Dashed lines are equipotential lines while solid lines are electric field lines. Click on one of the diagrams for further detail.

Electric Potential Energy Due to a Point Charge

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image082.png

    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image083.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image084.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image085.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image086.png

Electric Force from Electric Potential Energy

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image087.png

Electric Potential Due to a Point Charge

  • Electric potential (voltage) is the work per unit charge required to bring a charge from infinity to some point R in an electric field

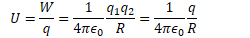
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image088.png

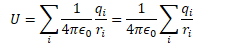
  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image089.png

Example 1: Electric Potential Due to a Point Charge

  • Find the electric potential at point P, located 3 meters away from a -2 C charge.

  • What is the electric potential energy of a 0.5 C charge situated at point P?

    -C

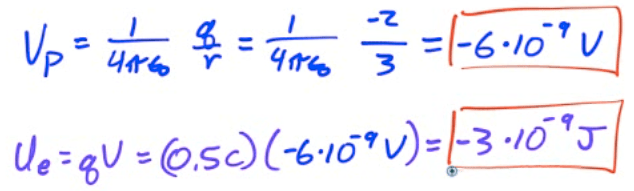
Example 2: Electric Potential Due to a Point Charge

  • Find the electric potential at the origin due to the three charges shown in the diagram. If an electron is placed at the origin, what potential energy does it possess?

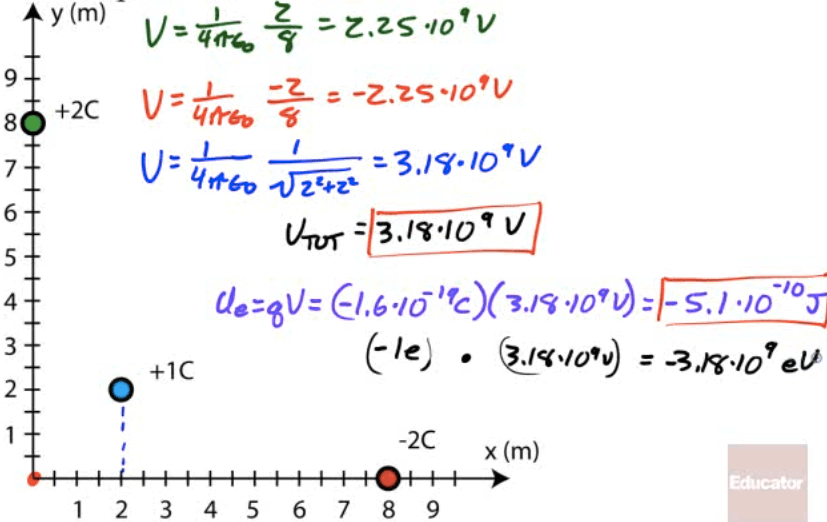
    9 8 7 6 5 4 3 2 1 1 -Z.zs : 3.1î•lOÎ b/ o 2 3 4 5 6 Gl,6 •lđ •łofv) (-1e) • - - -3.R•đev 7

Finding Electric Field from Electric Potential

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image092.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image093.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image094.png

Finding Electric Potential from Electric Field

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image095.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image096.png

  • C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image097.png

    Δν Ιώ 14

Example 3: Electric Potential Due to a Point Charges

Find the electric potential at the origin due to the following charges: '2bLC at (3,0); -51LC at (0,5); and IBIC at (4,4).

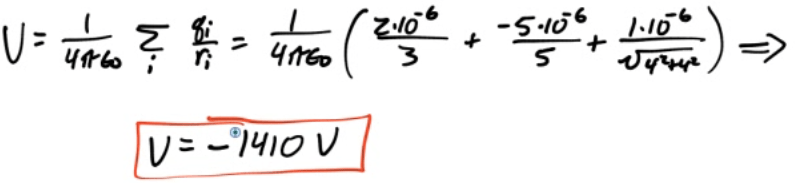
n Olhl€— = (l

Example 4: Electric Field from Potential

Given an electric potential of V(x)=5x2-7x, find the magnitude and direction of the electric field at x=3m. — é-/0x)

Example 5: Speed of an Electron Released in an Electric Field

An electron is released from rest in a uniform electric field of 500 N/C. What is its velocity after it has traveled one meter? : 1.33.18 % 7.1/00 '1k\*

Example 6: Work Required to Establish a Charge System

![Two point charges (5 VLC and 2 [LC) are placed 0.5 meters apart. How much work was required to establish the charge system? ](./media/image103.png)

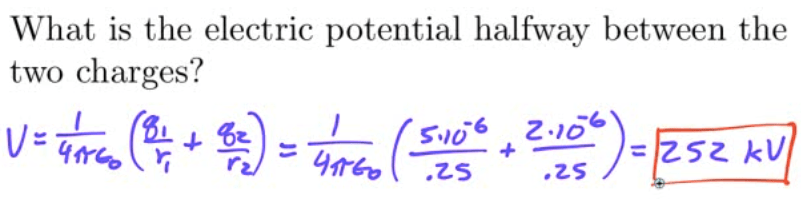
What is the electric potential halfway between the two charges? Z .10 .ZS sa kv

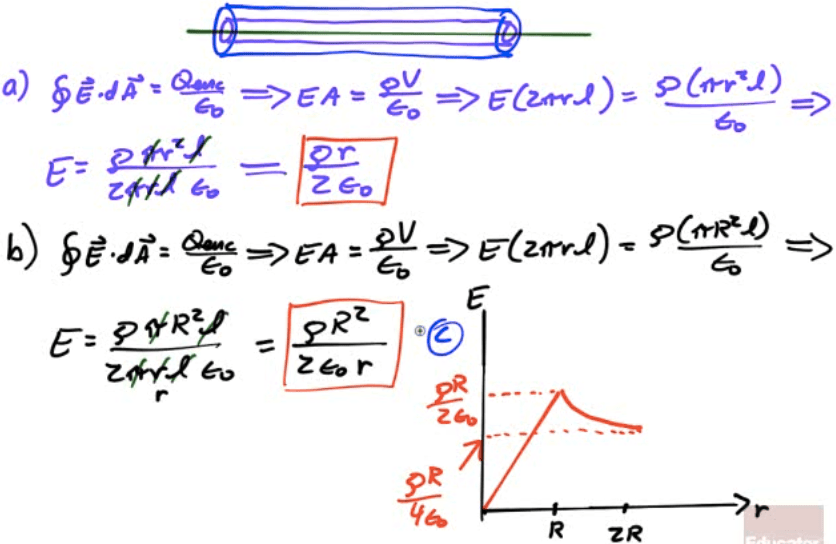
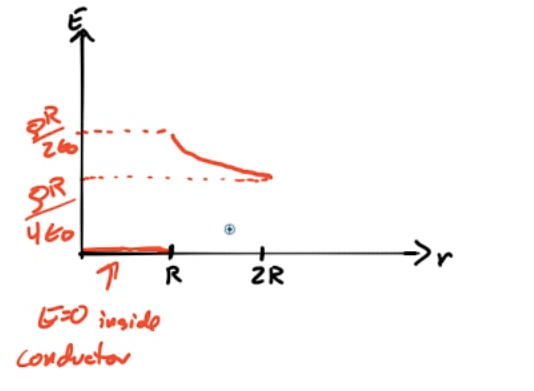
2013 Free Response Question 1

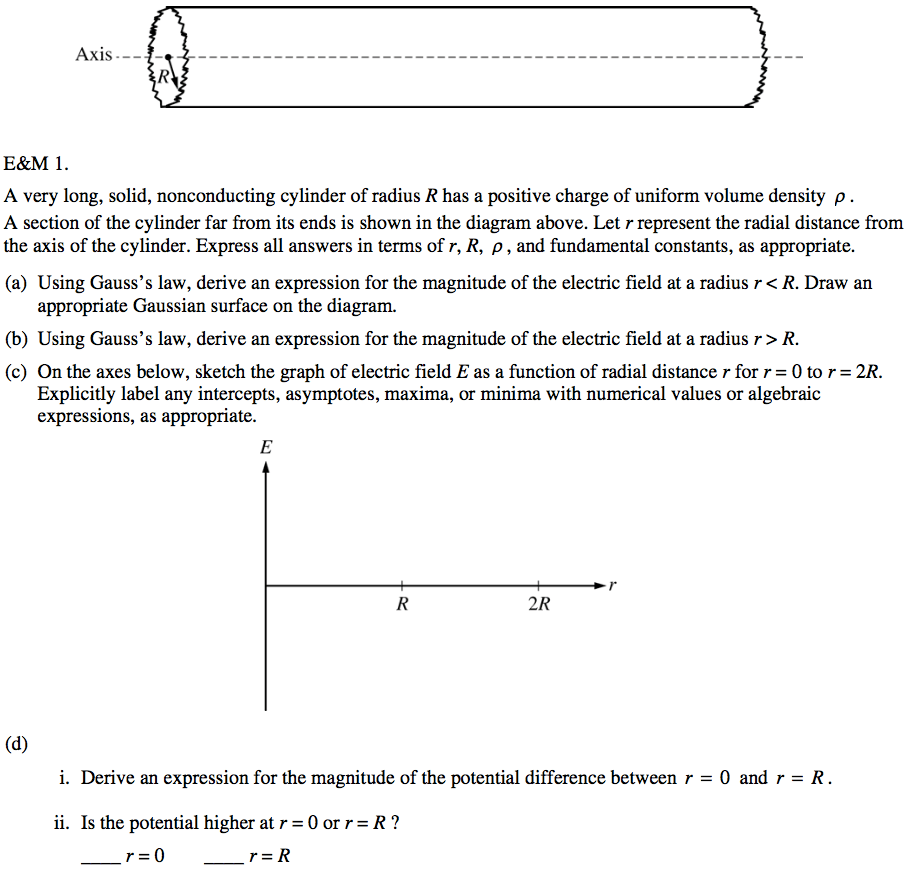
Axis.-- - A very long, solid, nonconducting cylinder of radius R has a positive charge of uniform volume density p . A section of the cylinder far from its ends is shown in the diagram above. Let r represent the radial distance from the axis of the cylinder. Express all answers in terms of r, R, p , and fundamental constants, as appropriate. (a) Using Gauss's law, derive an expression for the magnitude of the electric field ata radius r < R. Draw an appropriate Gaussian surface on the diagram. (b) Using Gauss's law, derive an expression for the magnitude of the electric field at a radius r > R. (c) On the axes below, sketch the graph of electric field E as a function of radial distance r for r = 0 to r = 2R. Explicitly label any intercepts, asymptotes, maxima, or minima with numerical values or algebraic expressions, as appropnate. (d) 2R i. Derive an expression for the magnitude of the potential difference between r ii. Is the potential higher at r = 0 or r = R ? O and r = R.

(e) The nonconducting cylinder is replaced with a conducting cylinder of the same shape and same linear charge density. On the axes below, sketch the electric field E as a function of r for r = 0 to r = 2R. Explicitly label any intercepts, asymptotes, maxima, or minima with numerical values or algebraic expressions, as appropriate. 2R

eo —>EčZffA)-

![[9-/nl 2-4 ](./media/image108.png)

نى هده: ملحم

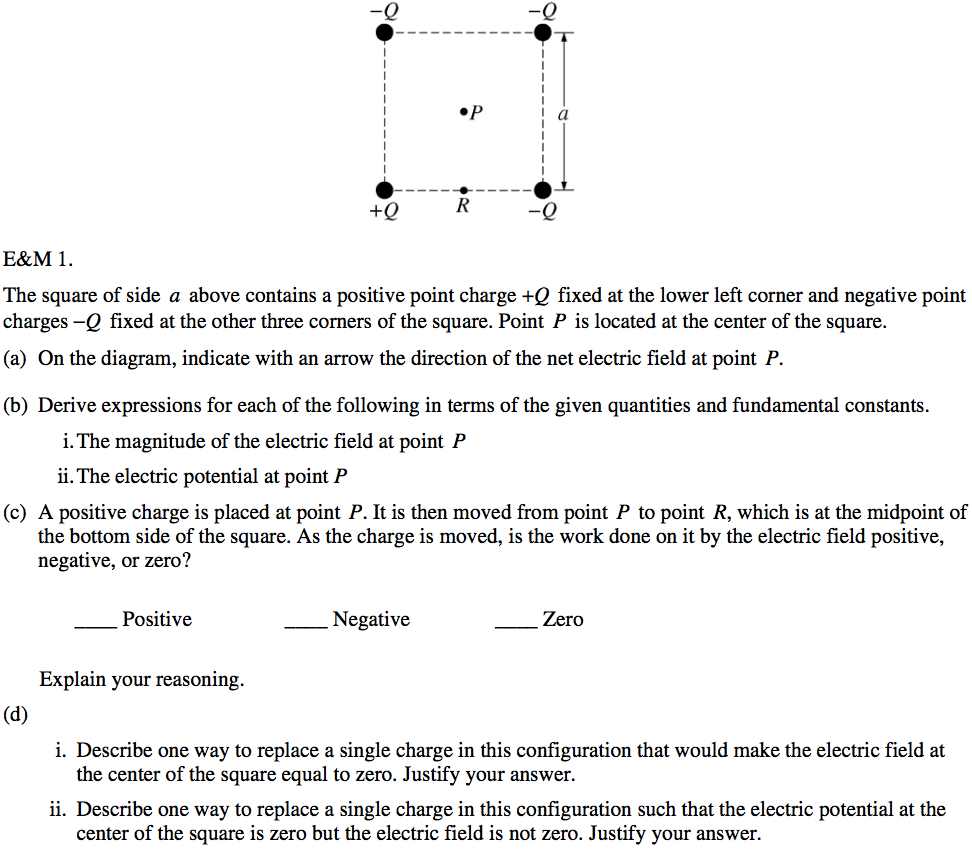
2006 Free Response Question 1

-Q R -Q -Q The square of side a above contains a positive point charge +Q fixed at the lower left corner and negative point charges —Q fixed at the other three corners of the square. Point P is located at the center of the square. (a) On the diagram, indicate with an arrow the direction of the net electric field at point P. (b) Derive expressions for each of the following in terms of the given quantities and fundamental constants. i. The magnitude of the electric field at point P ii. The electric potential at point P (c) A positive charge is placed at point P. It is then moved from point P to point R, which is at the midpoint of the bottom side of the square. As the charge is moved, is the work done on it by the electric field positive, negative, or zero? Positive Explain your reasoning. (d) Negative Zero i. Describe one way to replace a single charge in this configuration that would make the electric field at the center of the square equal to zero. Justify your answer. ii. Describe one way to replace a single charge in this configuration such that the electric potential at the center of the square is zero but the electric field is not zero. Justify your answer.

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image111.png

h os v+ 11 -F\!Od os

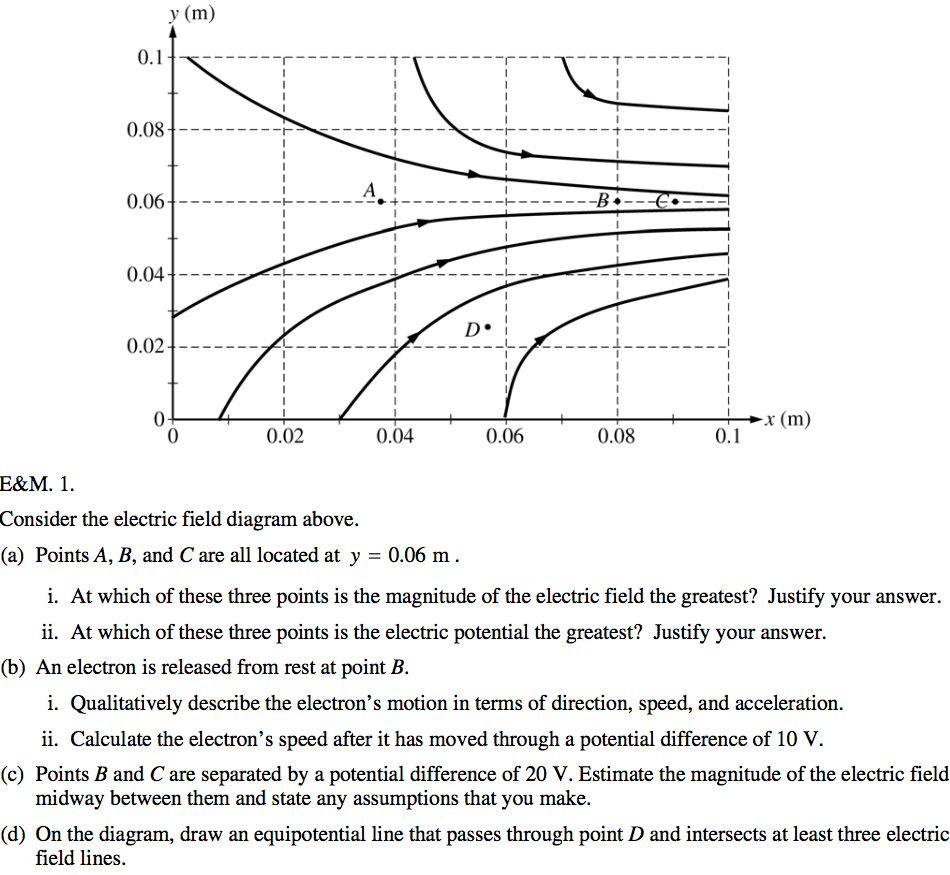
2005 Free Response Question 1

0.1 0.08 0.06 - 0.04 - 0.02 - 0.02 Consider the electric field diagram above. 0.04 0.06 0.08 0.1 (a) Points A, B, and C are all located at y = 0.06 m . i. At which of these three points is the magnitude of the electric field the greatest? Justify your answer. ii. At which of these three points is the electric potential the greatest? Justify your answer. (b) An electron is released from rest at point B. i. Qualitatively describe the electron's motion in terms of direction, speed, and acceleration. ii. Calculate the electron's speed after it has moved through a potential difference of 10 V. (c) Points B and C are separated by a potential difference of 20 V. Estimate the magnitude of the electric field midway between them and state any assumptions that you make. (d) On the diagram, draw an equipotential line that passes through point D and intersects at least three electric field lines.

(أم تامايه Q ٤ ولهع،اة هما وسمه (؟( •4, ثهF اوم مم ا او: سا نسما ـبلسهأهم ) دد حي ا ما لوهماو، اسمايم (ا منامة لمعه حلـمه مسيل لم عنفا ها ؟ بد . لءهمةىا وسم ا مهاا ه -٥اأهمة ذمهسه م ، وع مها هماها»،٥ ذ: ٥٥ ح (:: لونا ي -ار ا دح ء ل2 لل رى / ؛ ن جيىجإمم ح،.ـ٩٩،I يير (٥ يج ردة ممحح و-:س٩٩ يااه ي: س، E

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image115.png

2003 Free Response Question 1

A spherical cloud of charge of radius R contains a total charge +Q with a nonuniform volume charge density that varies according to the equation p(r) = PO(I for r R and p = O for r > R, where r is the distance from the center of the cloud. Express all algebraic answers in terms of Q, R, and fundamental constants. (a) (b) (c) (d) (e) Determine the following as a function of r for r > R. i. The magnitude E of the electric field ii. The electric potential V A proton is placed at point P shown above and released. Describe its motion for a long time after its release. An electron of charge magnitude e is now placed at point P, which is a distance r from the center of the sphere, and released. Determine the kinetic energy of the electron as a function of r as it strikes the cloud. Derive an expression for po . Determine the magnitude E of the electric field as a function of r for r R .

( «لا وديت؟- مرفي-، ررم. ته «د صاب (ا ت اان ينهيه ماه سحيم عمصامة ت (ياو،» : يا:يهاعن ما و:e٥sلا ما ( مسا تا ؛ ماة.علا مياه دت سهلا يتعهعيـتطهسهن

neé S

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image119.png

results matching ""

    No results matching ""